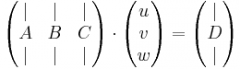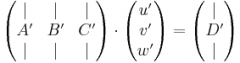Marschal
Großer Enumerator
Hallo Community,
Ich habe ein Problem was in kein Forum so richtig reinpasst, deshalb hab ichs mal im Coders Talk gepostet.
Ausgangspunkt:
(Ich erkläre es prinziepiell ohne zu sehr auf den Kram drum rum einzugehen)
Ich habe eine Kamera, die irgendwie im Raum angeordnet ist. Diese betrachtet eine Projektionsfläche (aus irgendeinem Winkel).
Vllt noch schnell was genau das werden soll. Im Prinziep ein Whiteboard, jedoch nur auf optischer Basis, dh keine touchfläche also, deswegen auch die Kamera.
Somit soll dann (mit einer Lichtquelle z.B.) auf der Projektionsfläche ein optisches Signal erfolgen. dieses Muss die Kamera erfassen (tut sie auch ) und in einen (für den Anfang "nur") Mouseklick auf dem mit dem Beamer verbundenen Rechner erfolgen.
) und in einen (für den Anfang "nur") Mouseklick auf dem mit dem Beamer verbundenen Rechner erfolgen.
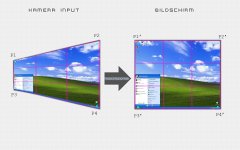
Hoffe es ist klar, was ich meine. Hab im Anhang eine einfache Darstellung des Aufbaus.
Mein Problem ist nun folgendes:
Ich brauche eine Mathematische rechen operation, die das (gezerrte Bild, welches die Kammera wahrnimmt, da sie ja irgendwie angeordnet ist) wieder in ein quadratisches (also Bilschirmauflösung) umrechnet.
Ich hatte mir eine 4-Punkt kalibrierung gedacht. Also, man geht mit dem Zeigegerät zur Projektionsfläche und klickt auf die 4 Eckpunkte. Somit erhält man auch vier Koordinaten von der Kamara (nähmlich die, wo die einzelnen Eckpunkte landen). Nach der Kalibrierung muss irgendeine Matrix vorhanden sein (so hab ich mir das gedacht) die dan jeden Beliebigen Punkt auf der Projektionsfläche auf den analogen Punkt auf dem Bildschrim umrechen.
Hier ist also eher ein logisches Problem, programmiert krieg ich das nähmlich, ich hab aber irgendwie Fehler in meinem Ansatz.
Ich würde mich sehr über Diskusion und Anregung freuen.
MfG
EDIT: Zum Bild. Es ist klar, der Beamer stellt ein Recheckiges Bild dar, so wies sein soll, die Kamera sieht jedoch ein ein gezertes Bild, also ein Trapez oder ähnliches. Hoffe es ist klar was gemeint ist, und dass jemand helfen kann
EDIT2: Auf dem zweiten Bild habe ich nochmal schematisch dargestellt worum es geht.
MfG
Ich habe ein Problem was in kein Forum so richtig reinpasst, deshalb hab ichs mal im Coders Talk gepostet.
Ausgangspunkt:
(Ich erkläre es prinziepiell ohne zu sehr auf den Kram drum rum einzugehen)
Ich habe eine Kamera, die irgendwie im Raum angeordnet ist. Diese betrachtet eine Projektionsfläche (aus irgendeinem Winkel).
Vllt noch schnell was genau das werden soll. Im Prinziep ein Whiteboard, jedoch nur auf optischer Basis, dh keine touchfläche also, deswegen auch die Kamera.
Somit soll dann (mit einer Lichtquelle z.B.) auf der Projektionsfläche ein optisches Signal erfolgen. dieses Muss die Kamera erfassen (tut sie auch
Hoffe es ist klar, was ich meine. Hab im Anhang eine einfache Darstellung des Aufbaus.
Mein Problem ist nun folgendes:
Ich brauche eine Mathematische rechen operation, die das (gezerrte Bild, welches die Kammera wahrnimmt, da sie ja irgendwie angeordnet ist) wieder in ein quadratisches (also Bilschirmauflösung) umrechnet.
Ich hatte mir eine 4-Punkt kalibrierung gedacht. Also, man geht mit dem Zeigegerät zur Projektionsfläche und klickt auf die 4 Eckpunkte. Somit erhält man auch vier Koordinaten von der Kamara (nähmlich die, wo die einzelnen Eckpunkte landen). Nach der Kalibrierung muss irgendeine Matrix vorhanden sein (so hab ich mir das gedacht) die dan jeden Beliebigen Punkt auf der Projektionsfläche auf den analogen Punkt auf dem Bildschrim umrechen.
Hier ist also eher ein logisches Problem, programmiert krieg ich das nähmlich, ich hab aber irgendwie Fehler in meinem Ansatz.
Ich würde mich sehr über Diskusion und Anregung freuen.
MfG
EDIT: Zum Bild. Es ist klar, der Beamer stellt ein Recheckiges Bild dar, so wies sein soll, die Kamera sieht jedoch ein ein gezertes Bild, also ein Trapez oder ähnliches. Hoffe es ist klar was gemeint ist, und dass jemand helfen kann
EDIT2: Auf dem zweiten Bild habe ich nochmal schematisch dargestellt worum es geht.
MfG
Anhänge
Zuletzt bearbeitet: