App installieren
So wird die App in iOS installiert
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: Diese Funktion ist in einigen Browsern möglicherweise nicht verfügbar.
Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
Du solltest ein Upgrade durchführen oder ein alternativer Browser verwenden.
[QUIZ#10] chmee (php)
- Themenstarter chmee
- Beginndatum
zu 1.Parsing der Positionsdaten:
Da ich nun nicht ständig code, ist sowas immer eine Aufgabe, die nicht einfach so und erst recht nicht optimiert gelöst wird. Aber folgendes RegEx-Pattern scheint seinen Job ganz gut zu machen.
$pattern = '
/([\d]+°)*([\d]+')*([\d]+")*([NS]{1})\s([\d]+°)*([\d]+')*([\d]+")*([WO]{1})\s([\D]+)/x
';
Es bleiben die Einheitenzeichen drin, aber das ist ein kleines Problem für danach. Wenn String!=0, dann eben hinten ein Zeichen weg. Vorteilhaft ist auch, dass die Arraygröße gleich bleibt, auch wenn Untereinheiten fehlen.
Array[1] bis [3] ° ' "
Array[4] Breite N oder S
Array[5] bis [7] ° ' "
Array[8] Länge W oder O
Array[9] Stadt
Da ich nun nicht ständig code, ist sowas immer eine Aufgabe, die nicht einfach so und erst recht nicht optimiert gelöst wird. Aber folgendes RegEx-Pattern scheint seinen Job ganz gut zu machen.
$pattern = '
/([\d]+°)*([\d]+')*([\d]+")*([NS]{1})\s([\d]+°)*([\d]+')*([\d]+")*([WO]{1})\s([\D]+)/x
';
Es bleiben die Einheitenzeichen drin, aber das ist ein kleines Problem für danach. Wenn String!=0, dann eben hinten ein Zeichen weg. Vorteilhaft ist auch, dass die Arraygröße gleich bleibt, auch wenn Untereinheiten fehlen.
Array[1] bis [3] ° ' "
Array[4] Breite N oder S
Array[5] bis [7] ° ' "
Array[8] Länge W oder O
Array[9] Stadt
Nun denn.
Gegeben 1:
2 Punkte, die auf einer Kugel liegen, beschreiben ihre kürzeste Entfernung mittels eines Großkreis-Segments, dem sogenannten Orthodrom. Haversine war mir unbekannt, aber das ist doch ein hilfreicher Tip.
Gegeben 2:
Der Radius der Erde wird mit 6371,01km oder 3447,07Seemeilen festgelegt.
Die Haversine-Formel übernommen :
(man muss nicht immer jede Formel verstehen, in diesem Fall übernehme ich sie einfach)
Code:
R = 6371;
dlon = deg2rad(B_lon - A_lon);
dlat = deg2rad(B_lat - A_lat);
a = (sin(dlat/2))^2 + cos(deg2rad(A_lat)) * cos(deg2rad(B_lat)) * (sin(dlon/2))^2;
c = 2 * asin(min(1,sqrt(a)));
d = R * c;Der lustige Teil ist ja eher, die entstehenden Orthodrome mit Wegpunkten zu beschreiben. Vielleicht aollte man sich auf eine Linie begrenzen, die alle 2° einen Punkt bekommt. Das sollte zur Visualisierung hinreichend genau sein.
Mom: Muss an den anderen Rechner
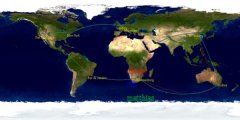
Hier also der Code für die SVG mit Positionskreuzen und den Loxodromen.In den SVG-Comments stehen die Entfernungen.
PHP:
<?php header("Content-type: image/svg+xml");
echo '<?xml version="1.0" encoding="iso-8859-1"?>';
echo '<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">';
echo '<svg version="1.1" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" width="1024" height="512" stroke="red" fill="none" viewBox="-180 -90 360 180" stroke-width="0.3">';
echo "<defs><g id='Kreuz'>";
echo '<line x1="-1" y1="-1" x2="1" y2="1" />';
echo '<line x1="-1" y1="1" x2="1" y2="-1" />';
echo'</g></defs>';
echo '<image x="-180" y="-90" width="360" height="180" xlink:href="http://veimages.gsfc.nasa.gov/2430/land_ocean_ice_2048.jpg" />';
echo "\n\r";
$Erdradius=6371;
$Daten=
array(
"48°8'N 11°34'O München",
"25°15'N 55°18'O Dubai",
"39°54'50\"N 116°23'30\"O Peking",
"33°51'S 151°12'O Sydney",
"26°12'S 28°4'O Johannesburg",
"22°54'S 43°12'W Rio de Janeiro",
"37°47'N 122°25'W San Francisco",
"40°43'N 74°0'W New York",
"51°31'N 0°7'W London",
"48°8'N 11°34'O München"
);
$Punkte=count($Daten);
for($i=0;$i<($Punkte-1);$i++)
{
$pattern = "/([\d]+°)*([\d]+')*([\d]+\")*([NS]{1})\s([\d]+°)*([\d]+')*([\d]+\")*([WO]{1})\s([\D]+)/x";
preg_match($pattern,$Daten[$i],$ergA);
preg_match($pattern,$Daten[$i+1],$ergB);
$A_lat=intval(str_replace("°","",$ergA[1]))+intval(str_replace("'","",$ergA[2]))/60+intval(str_replace("\"","",$ergA[3]))/3600;
$A_lon=intval(str_replace("°","",$ergA[5]))+intval(str_replace("'","",$ergA[6]))/60+intval(str_replace("\"","",$ergA[7]))/3600;
$B_lat=intval(str_replace("°","",$ergB[1]))+intval(str_replace("'","",$ergB[2]))/60+intval(str_replace("\"","",$ergB[3]))/3600;
$B_lon=intval(str_replace("°","",$ergB[5]))+intval(str_replace("'","",$ergB[6]))/60+intval(str_replace("\"","",$ergB[7]))/3600;
$dlon = deg2rad($B_lon - $A_lon);
$dlat = deg2rad($B_lat - $A_lat);
$a = pow(sin($dlat/2),2) + cos(deg2rad($A_lat)) * cos(deg2rad($B_lat)) * pow(sin($dlon/2),2);
$c = 2 * asin(min(1,sqrt($a)));
$d = $Erdradius * $c;
echo "<!-- ".$ergA[9].", ".$ergB[9]." = ".$d."km = ".$d*0.621." meilen -->";
echo "\n\r";
// Wenn N lat Vorzeichen umdrehen, lon W vice versa
if($ergA[4]=="N"){$A_lat=-$A_lat;}
if($ergA[8]=="W"){$A_lon=-$A_lon;}
echo '<use xlink:href="#Kreuz" transform="translate('.$A_lon.' '.$A_lat.')" />';
if($ergB[4]=="N"){$B_lat=-$B_lat;}
if($ergB[8]=="W"){$B_lon=-$B_lon;}
echo '<line x1="'.$A_lon.'" y1="'.$A_lat.'" x2="'.$B_lon.'" y2="'.$B_lat.'"/>';
echo "\n\r";
}
?>
</svg>So, nach einer Pause mit Rotwein und Donauwelle fiel mir Folgendes ein:
Ein Großkreis -egal welcher Ausrichtung- beschreibt auf einer winkeltreuen Karte "möglicherweise" immer eine Sinuswelle mit der Frequenz 1, einem verschiedenen Hub und verschiedener Phase.
 natürlich sind "senkrechte Großkreise", die durch die Pole laufen, davon ausgeschlossen.
natürlich sind "senkrechte Großkreise", die durch die Pole laufen, davon ausgeschlossen.
Ergo : Mit den zwei Punkten muss "nur" eine Sinuskurve gefunden werden, Fix ist die Frequenz, variabel sind Amplitude und Phasenverschiebung.
EDIT: 00.10Uhr - Nee eigentlich nicht 2 Gedanken, die nicht in diese These hineinpassen :
2 Gedanken, die nicht in diese These hineinpassen :
1. 2 Beliebige Punkte in einem Koordinatenkreuz x(-180,180) und y(-90,90) können nicht durch eine Sinusfunktion mit der Frequenz 1 und einer Amplitude <90 beschrieben werden.
2. Umso näher die Punkte gen Pole, desto hysteretischer werden sie.
-> Parabeln
Ach ja, noch ein Link: http://freenet-homepage.de/stwessels/unterricht/navigation/gc.pdf
Ein Großkreis -egal welcher Ausrichtung- beschreibt auf einer winkeltreuen Karte "möglicherweise" immer eine Sinuswelle mit der Frequenz 1, einem verschiedenen Hub und verschiedener Phase.
Ergo : Mit den zwei Punkten muss "nur" eine Sinuskurve gefunden werden, Fix ist die Frequenz, variabel sind Amplitude und Phasenverschiebung.
EDIT: 00.10Uhr - Nee eigentlich nicht
1. 2 Beliebige Punkte in einem Koordinatenkreuz x(-180,180) und y(-90,90) können nicht durch eine Sinusfunktion mit der Frequenz 1 und einer Amplitude <90 beschrieben werden.
2. Umso näher die Punkte gen Pole, desto hysteretischer werden sie.
-> Parabeln
Ach ja, noch ein Link: http://freenet-homepage.de/stwessels/unterricht/navigation/gc.pdf
Nun denn, Aufgabe 1:
Die Orthodrome habe ich einfach nur mit dem Startpunkt, dem Initialwinkel und variablen Distanzen aufgebaut, als L-Path in SVG. Alle Formeln sind von http://www.yourhomenow.com/house/haversine.html. Die Daten ließen sich ja recht unkompliziert aus einer txt-Datei rauslesen, der Einfachheit halber ist es bei mir gleich ein Array, womit der Code als Copy&Paste lauffähig ist. Ich hab am Dienstag auch wieder aufgehört, ergo könnte die Pazifiküberquerung mies aussehen, aber : Ich hab was gelernt Über SVG, Großkreise und Orthodrome..
Über SVG, Großkreise und Orthodrome..
104 Zeilen 
Die Orthodrome habe ich einfach nur mit dem Startpunkt, dem Initialwinkel und variablen Distanzen aufgebaut, als L-Path in SVG. Alle Formeln sind von http://www.yourhomenow.com/house/haversine.html. Die Daten ließen sich ja recht unkompliziert aus einer txt-Datei rauslesen, der Einfachheit halber ist es bei mir gleich ein Array, womit der Code als Copy&Paste lauffähig ist. Ich hab am Dienstag auch wieder aufgehört, ergo könnte die Pazifiküberquerung mies aussehen, aber : Ich hab was gelernt
PHP:
<?php header("Content-type: image/svg+xml");
echo '<?xml version="1.0" encoding="iso-8859-1"?>';
?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/REC-SVG-20010904/DTD/svg10.dtd">
<svg version="1.1" xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink" width="1024" height="512"
stroke="red" fill="none" viewBox="-180 -90 360 180" stroke-width="0.3">
<defs><g id='Kreuz'>
<line x1="-1" y1="-1" x2="1" y2="1" />
<line x1="-1" y1="1" x2="1" y2="-1" />
</g></defs>
<image x="-180" y="-90" width="360" height="180" xlink:href="http://veimages.gsfc.nasa.gov/2430/land_ocean_ice_2048.jpg" />
<?php
echo "\n\r";
$Erdradius=6371;
$Daten=
array(
"48°8'N 11°34'O München",
"25°15'N 55°18'O Dubai",
"39°54'50\"N 116°23'30\"O Peking",
"33°51'S 151°12'O Sydney",
"26°12'S 28°4'O Johannesburg",
"22°54'S 43°12'W Rio de Janeiro",
"37°47'N 122°25'W San Francisco",
"40°43'N 74°0'W New York",
"51°31'N 0°7'W London",
"48°8'N 11°34'O München"
);
$Punkte=count($Daten);
for($i=0;$i<($Punkte-1);$i++)
{
$pattern = "/([\d]+°)*([\d]+')*([\d]+\")*([NS]{1})\s([\d]+°)*([\d]+')*([\d]+\")*([WO]{1})\s([\D]+)/x";
preg_match($pattern,$Daten[$i],$ergA);
preg_match($pattern,$Daten[$i+1],$ergB);
//Einheiten rausnehmen und Winkel berechnen
$A_lat=intval(str_replace("°","",$ergA[1]))+intval(str_replace("'","",$ergA[2]))/60+intval(str_replace("\"","",$ergA[3]))/3600;
$A_lon=intval(str_replace("°","",$ergA[5]))+intval(str_replace("'","",$ergA[6]))/60+intval(str_replace("\"","",$ergA[7]))/3600;
$B_lat=intval(str_replace("°","",$ergB[1]))+intval(str_replace("'","",$ergB[2]))/60+intval(str_replace("\"","",$ergB[3]))/3600;
$B_lon=intval(str_replace("°","",$ergB[5]))+intval(str_replace("'","",$ergB[6]))/60+intval(str_replace("\"","",$ergB[7]))/3600;
// Grad zu rad
$A_lat=deg2rad($A_lat);
$A_lon=deg2rad($A_lon);
$B_lat=deg2rad($B_lat);
$B_lon=deg2rad($B_lon);
// Vorzeichen umkehren für N lat und W lon
if($ergA[4]=="N"){$A_lat=-$A_lat;}
if($ergA[8]=="W"){$A_lon=-$A_lon;}
// für die Loxodrome (und die Entfernung d) auch den 2.Punkt bearbeiten
if($ergB[4]=="N"){$B_lat=-$B_lat;}
if($ergB[8]=="W"){$B_lon=-$B_lon;}
// Haversine
$dlon = $B_lon - $A_lon;
$dlat = $B_lat - $A_lat;
$a = pow(sin($dlat/2),2) + cos($A_lat) * cos($B_lat) * pow(sin($dlon/2),2);
$c = 2 * asin(min(1,sqrt($a)));
$d = $Erdradius * $c;
// Startwinkel des Fluges
$y = sin($dlon) * cos($B_lat);
$x = cos($A_lat)*sin($B_lat) -sin($A_lat)*cos($B_lat)*cos($dlon);
$brng = atan2($y, $x);
// Comment in der SVG
echo "<!-- ".$ergA[9].", ".$ergB[9]." = ".$d."km = ".$d*0.621." meilen & Startwinkel :".rad2deg($brng)."° -->";
echo "\n\r";
// Jeder nur ein Kreuz
echo '<use xlink:href="#Kreuz" transform="translate('.rad2deg($A_lon).' '.rad2deg($A_lat).')" />';
echo "\n\r";
//Loxodrom in Gruen zeichnen
echo '<line x1="'.rad2deg($A_lon).'" y1="'.rad2deg($A_lat).'" x2="'.rad2deg($B_lon).'" y2="'.rad2deg($B_lat).'" ';
echo 'style="stroke:rgb(0,255,0);stroke-width:0.2"/>';
echo "\n\r";
//Orthodrome zeichnen - bestehend aus $sAnz Stützpunkten
$sAnz=20;
$ddist=$d/$sAnz;
// Startpunkt der SVG-Linie
echo '<path d="M'.rad2deg($A_lon).' '.rad2deg($A_lat);
for($multi=0;$multi<($sAnz+1);$multi++)
{
//Wegpunkt anhand Initialwinkel und Entfernung
$ddd=$ddist*$multi;
$ddlat = asin( sin($A_lat)*cos($ddd/$Erdradius) + cos($A_lat)*sin($ddd/$Erdradius)*cos($brng) );
$ddlon = $A_lon + atan2(sin($brng)*sin($ddd/$Erdradius)*cos($A_lat),cos($ddd/$Erdradius)-sin($A_lat)*sin($B_lat));
// weiteren Punkt in der SVG-Path setzen
echo ' L'.number_format(rad2deg($ddlon),1).' '.number_format(rad2deg($ddlat),1);
}
//SVG Path schließen
echo '"/>';
echo "\n\r";
}
?>
</svg>Matthias Reitinger
ɐɯıǝɹ
Hallo chmee,
die tagebuchartige Aufmachung deiner Abgabe finde ich ja mal klasse Werd mir deine Lösung (und die verlinkten Seiten) nachher mal genauer anschauen, du hast es anscheinend etwas anders gelöst als ich.
Werd mir deine Lösung (und die verlinkten Seiten) nachher mal genauer anschauen, du hast es anscheinend etwas anders gelöst als ich.
Grüße,
Matthias
die tagebuchartige Aufmachung deiner Abgabe finde ich ja mal klasse
Grüße,
Matthias
Matthias Reitinger
ɐɯıǝɹ
Hallo chmee,
ich hab mir deinen Ansatz jetzt mal näher angeschaut. Wenn ich das richtig sehe, berechnest du die Wegpunkte über die Formel unter „Destination point given distance and bearing from start point“ auf http://www.yourhomenow.com/house/haversine.html? Das ist natürlich auch keine schlechte Idee. Ich hab ja schon einen Absatz früher aufgehört zu lesen und hab mich mit der Formel zum Midpoint zufrieden gegeben Aber interessant zu sehen, wie jeder ein bisschen anders zum Ziel gekommen ist.
Aber interessant zu sehen, wie jeder ein bisschen anders zum Ziel gekommen ist.
Dann will ich auch gleich noch ein bisschen (hoffentlich konstruktiv) rumkritisieren. Was mir zu allererst aufgefallen ist: dein Algorithmus berechnet teils andere Wege als meine. Ich weiß nicht genau, woran das liegt, aber hier mal ein Bild, das die Unterschiede aufzeigt (rot: deine Route, grün: meine Route):
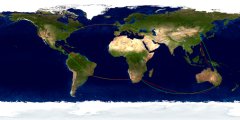
Dann zum regulären Ausdruck. Den könnte man zuerst mal etwas verkürzen, indem man unnötige Teile weglässt:
Als nächstes würde ich den *-Quantifizierer jeweils durch ein ? ersetzen. Leerzeichen kann man ruhig auch mehrere zulassen und der Ortsname könnte theoretisch auch eine Ziffer enthalten. Nach dem DRY-Prinzip sollte man den wiederholten Teil für die Grad-Angabe noch rausziehen:
Und das ganze am besten noch aus der Schleife rausziehen.
Bei der Berechnung von Breite und Höhe hast du dann wieder sehr viel duplizierten Code drinnen – sollte man vielleicht in eine Funktion auslagern.
Das Entfernen von °, ', " vor der Anwendung von intval kannst du auch weglassen, intval ignoriert diese Zeichen am Schluss sowieso.
In der Schleife zur Erzeugung der Wegpunkte könnte man die konstanten Faktoren vielleicht noch vorberechnen. Sollte aber nicht so den riesigen Unterschied bei der vermutlich ohnehin schon ziemlich kurzen Ausführungszeit machen.
So, mehr fällt mir gerade nicht auf. Hoffe das war jetzt nicht zu viel Kritik
Grüße, Matthias
ich hab mir deinen Ansatz jetzt mal näher angeschaut. Wenn ich das richtig sehe, berechnest du die Wegpunkte über die Formel unter „Destination point given distance and bearing from start point“ auf http://www.yourhomenow.com/house/haversine.html? Das ist natürlich auch keine schlechte Idee. Ich hab ja schon einen Absatz früher aufgehört zu lesen und hab mich mit der Formel zum Midpoint zufrieden gegeben
Dann will ich auch gleich noch ein bisschen (hoffentlich konstruktiv) rumkritisieren. Was mir zu allererst aufgefallen ist: dein Algorithmus berechnet teils andere Wege als meine. Ich weiß nicht genau, woran das liegt, aber hier mal ein Bild, das die Unterschiede aufzeigt (rot: deine Route, grün: meine Route):

Dann zum regulären Ausdruck. Den könnte man zuerst mal etwas verkürzen, indem man unnötige Teile weglässt:
Code:
/(\d+°)*(\d+')*(\d+\")*([NS])\s(\d+°)*(\d+')*(\d+\")*([WO])\s(\D+)/
PHP:
$degree_pattern = "(\d+°)?(\d+')?(\d+\")?";
$pattern = "/^\s*$degree_pattern([NS])\s+$degree_pattern([WO])\s+(.+)\$/"Bei der Berechnung von Breite und Höhe hast du dann wieder sehr viel duplizierten Code drinnen – sollte man vielleicht in eine Funktion auslagern.
Das Entfernen von °, ', " vor der Anwendung von intval kannst du auch weglassen, intval ignoriert diese Zeichen am Schluss sowieso.
In der Schleife zur Erzeugung der Wegpunkte könnte man die konstanten Faktoren vielleicht noch vorberechnen. Sollte aber nicht so den riesigen Unterschied bei der vermutlich ohnehin schon ziemlich kurzen Ausführungszeit machen.
So, mehr fällt mir gerade nicht auf. Hoffe das war jetzt nicht zu viel Kritik
Grüße, Matthias
Das nett, danke.. Der Unterschied der Wege ist interessant, indeed.. Optimieren wollt ich nicht, so ist der Code recht gut nachvollziehbar, sequentiell jedenfalls. Und ja, das Pattern kann man auf jeden Fall verbessern..
Interessant wäre auch noch ein möglicher Distanzunterschied zwischen meiner Berechnung, deiner und einer unabhängigen Seite. (Obwohl diese Formel die Klarste ist). Auch die Anzeige einer Routenberechnugn einer anderen Seite wäre interessant. Ich stöber mal später.
mfg chmee
p.s.: Ja, diese Formel zur Wegbeschreibung ist es.
Interessant wäre auch noch ein möglicher Distanzunterschied zwischen meiner Berechnung, deiner und einer unabhängigen Seite. (Obwohl diese Formel die Klarste ist). Auch die Anzeige einer Routenberechnugn einer anderen Seite wäre interessant. Ich stöber mal später.
mfg chmee
p.s.: Ja, diese Formel zur Wegbeschreibung ist es.