hi Leute,
ich hänge immer noch bei den Bäumen.
Ziel: Diesen Ausdruck ((2+6)/(3*4))) -> [2, 6, +, 3, 4, *, / ] so umwandeln
Also was ich hab sind OP-Methoden(Expressions) die als Knoten dienen. Und Cont der als Blatt dient.
Die Bedingung der Aufgabe ist das ganze in Stack-Form zu lösen (grob gesagt).
Also so wie ich es verstanden hab . Man durchläuft (traversiert) durch die Blätter und fasst diesen mit dem Knoten zusammen...Diese Form nennt man glaub ich Postfix. z.B (2+3) -> 2,3,+
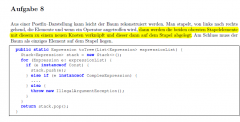
Ich hab die relevante Methode über die ich spreche oben im Quellcode Kommentiert.
Problem-Nummer 1. = Wieso bekomme ich -8 und nicht einfach 8 ausgegeben? (wenn ich das Programm ausführe)
Problem-Nummer 2. = Zeile 204 ( zwei Zahlen zusammenführen) ich hab da sowas geschriebn :
müsste es aber nicht so heißen
Problem-Nummer 3. = Findet ihr noch Fehler? Oder könnt ihr mir etwas weiter bringen. Ich will keine lösung. Vielleicht erklärt ihr mir einfach nur ein denk Fehler.
Vielen Dank, schon mal !
ich hänge immer noch bei den Bäumen.
Ziel: Diesen Ausdruck ((2+6)/(3*4))) -> [2, 6, +, 3, 4, *, / ] so umwandeln
Also was ich hab sind OP-Methoden(Expressions) die als Knoten dienen. Und Cont der als Blatt dient.
Die Bedingung der Aufgabe ist das ganze in Stack-Form zu lösen (grob gesagt).
Also so wie ich es verstanden hab . Man durchläuft (traversiert) durch die Blätter und fasst diesen mit dem Knoten zusammen...Diese Form nennt man glaub ich Postfix. z.B (2+3) -> 2,3,+
Ich hab die relevante Methode über die ich spreche oben im Quellcode Kommentiert.
Problem-Nummer 1. = Wieso bekomme ich -8 und nicht einfach 8 ausgegeben? (wenn ich das Programm ausführe)
Problem-Nummer 2. = Zeile 204 ( zwei Zahlen zusammenführen) ich hab da sowas geschriebn :
Code:
result.push(new Mult(tempZ1, tempZ2));
Code:
result.push(new Const( new Mult(tempZ1, tempZ2)));Vielen Dank, schon mal !
Zuletzt bearbeitet: