Hallo zusammen,
ich habe folgendes Problem:
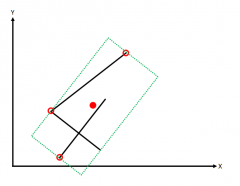
Stellt euch ein beliebiges Zeichen als gerade Linien in einem zwei Dimensionalen Koordinatensystem vor. Das Zeichen kann um einen beliebigen Winkel gedreht und an einer beliebigen Koordinate positioniert sein. Im Vorfeld gegeben hat man die Minimal- und Maximalwerte zu X und Y (Unausgefüllte rote Kreise in der Grafik), den Mittelpunkt (Ausgefüllter Kreis in der Grafik)und den Winkel um wie viel Grad das Zeichen gedreht ist.
Meine Frage lautet nun: Kann man sich anhand dieser Werte die Eckpunkte eines umschließenden Rechtecks berechnen (Gestrichelte grüne Linien in der Grafik)?
Zur besseren Vorstellung:
ich habe folgendes Problem:
Stellt euch ein beliebiges Zeichen als gerade Linien in einem zwei Dimensionalen Koordinatensystem vor. Das Zeichen kann um einen beliebigen Winkel gedreht und an einer beliebigen Koordinate positioniert sein. Im Vorfeld gegeben hat man die Minimal- und Maximalwerte zu X und Y (Unausgefüllte rote Kreise in der Grafik), den Mittelpunkt (Ausgefüllter Kreis in der Grafik)und den Winkel um wie viel Grad das Zeichen gedreht ist.
Meine Frage lautet nun: Kann man sich anhand dieser Werte die Eckpunkte eines umschließenden Rechtecks berechnen (Gestrichelte grüne Linien in der Grafik)?
Zur besseren Vorstellung: