Thomas Darimont
Erfahrenes Mitglied
Hallo,
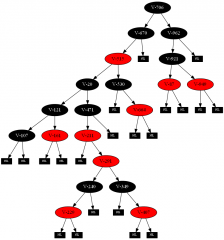
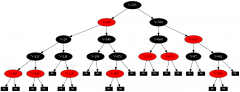
hier mal ein Beispiel für eine Rot-Schwarz Baum Implementierung in Java:
//EDIT dies ist eine Fehlerbereinigte Version -- siehe Erklärung unten
http://de.wikipedia.org/wiki/Rot-Schwarz-Baum
Gruß Tom
hier mal ein Beispiel für eine Rot-Schwarz Baum Implementierung in Java:
//EDIT dies ist eine Fehlerbereinigte Version -- siehe Erklärung unten
http://de.wikipedia.org/wiki/Rot-Schwarz-Baum
Java:
package de.tutorials;
import java.util.BitSet;
import java.util.Random;
/**
* @author Thomas.Darimont
*
*/
public class RedBlackTree<TKey extends Comparable<TKey>, TValue> {
private class Node {
private Node left, right;
private boolean color;
private TKey key;
private TValue value;
public Node(TKey key, TValue value, boolean color) {
this.key = key;
this.value = value;
this.color = color;
}
@Override
public String toString() {
return key + ": value " + (color ? "R" : "B");
}
}
private static final boolean RED = true;
private static final boolean BLACK = false;
private Node root;
public TValue get(TKey key) {
Node node = root;
while (node != null) {
int cmp = key.compareTo(node.key);
if (cmp < 0) {
node = node.left;
} else if (cmp > 0) {
node = node.right;
} else if (cmp == 0) {
return node.value;
}
}
return null;
}
private boolean isRed(Node node) {
if (node == null) {
return false;
}
return node.color;
}
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
return x;
}
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
return x;
}
private Node insert(Node node, TKey key, TValue value, boolean isRed) {
if (node == null) {
return new Node(key, value, RED); // RED was isRed before
}
if (isRed(node.left) && isRed(node.right)) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
int cmp = key.compareTo(node.key);
if (cmp < 0) {
node.left = insert(node.left, key, value, BLACK); // /*BLACK was
// isRed
// before*/
if (isRed(node) && isRed(node.left) && isRed) {
node = rotateRight(node);
}
if (isRed(node.left) && isRed(node.left.left)) {
node = rotateRight(node);
node.color = BLACK;
node.right.color = RED;
}
} else {
node.right = insert(node.right, key, value, RED);
if (isRed(node) && isRed(node.right) && !isRed) {
node = rotateLeft(node);
}
if (isRed(node.right) && isRed(node.right.right)) {
node = rotateLeft(node);
node.color = BLACK;
node.left.color = RED;
}
}
return node;
}
public void insert(TKey key, TValue value) {
this.root = insert(this.root, key, value, BLACK);
this.root.color = BLACK;
}
private void printDotGraph() {
System.out.println("//2-3-4 Red-Black Tree in graphviz dot-Format:");
printDotNode(root, true, 0);
}
private void printDotNode(Node node, boolean isRoot, int index) {
if (isRoot) {
System.out.printf("digraph g0 {%n");
System.out.printf("node [height=.1, style=filled];%n");
}
if (node != null) {
System.out
.printf("node%s_%s[label=\"%s\", color=black, fillcolor=%s, fontcolor=%s];%n",
index, node.key, node.value, isRed(node) ? "red"
: "black", isRed(node) ? "black" : "white");
if (node.left != null) {
printDotNode(node.left, false, index + 1);
System.out.printf("node%s_%s -> node%s_%s;%n", index, node.key,
index + 1, node.left.key);
} else {
System.out
.printf("nil_node_l_%s_%s[ width=.3, fontsize=7, label=\"NIL\", color=black, fontcolor=white, shape=record ];%n",
index, node.key);
System.out.printf("node%s_%s -> nil_node_l_%s_%s;%n", index,
node.key, index, node.key);
}
if (node.right != null) {
printDotNode(node.right, false, index + 1);
System.out.printf("node%s_%s -> node%s_%s;%n", index, node.key,
index + 1, node.right.key);
} else {
System.out
.printf("nil_node_r_%s_%s[ width=.3, fontsize=7, label=\"NIL\", color=black, fontcolor=white, shape=record ];%n",
index, node.key);
System.out.printf("node%s_%s -> nil_node_r_%s_%s;%n", index,
node.key, index, node.key);
}
} else {
System.out
.printf("nil_node_root_%s[width=.3, fontsize=7, label=\"NIL\", color=black, fontcolor=white, shape=record ];%n",
index);
}
if (isRoot) {
System.out.printf("}");
}
}
private static void outputRedBlackTreeWithRandomElements(int elementCount,
int seed, int maxRandomNumberExclusive) {
System.out.println("//RedBack_" + elementCount + "_elements");
RedBlackTree<String, String> tree = new RedBlackTree<String, String>();
Random random = new Random(seed);
BitSet alreadySeen = new BitSet(maxRandomNumberExclusive);
for (int i = 0; i < elementCount;) {
int value = random.nextInt(maxRandomNumberExclusive);
if (!alreadySeen.get(value)) {
alreadySeen.set(value);
i++;
tree.insert(String.valueOf(value), "V-" + String.valueOf(value));
}
}
tree.printDotGraph();
}
public static void main(String[] args) {
outputRedBlackTreeWithRandomElements(20, 4711, 1000);
//outputRedBlackTreeWithRandomElements(100, 4711, 1000);
//outputRedBlackTreeWithRandomElements(350, 4711, 1000);
}
}Gruß Tom
und ich bin auch noch Anfänger... 
schau doch mal bitte nach, ob die Fehler auch aus deiner Sicht behoben sind.
