Hallo alle zusammen!
Ich suche einen Algorithmus zum berechnen eines Rechtecks, welches den maximalen Flächeninhalt zweier übereinanderliegenden Rechtecke hat.
Beispiel:
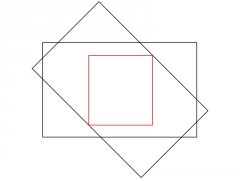
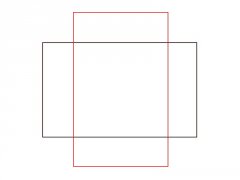
2 Rechtecke der selben Größe (ja, immer der selben Größe), liegen anfangs genau aufeinander. Wenn ich den Algorithmus nun anwende, sollte dieser mir ein Rechteck von der Größe der anderen beiden zurückgeben.
Jetzt drehe ich eines der beiden Rechtecke um X Grad um den Mittelpunkt von sich selbst.
Nun soll der Algorithmus mir die Koordinaten eines Rechtecks zurückgeben. Dieses Rechteck darf nur aus einer Fläche bestehen, welche das gedrehte Ursprungsrechteck vollständig enthält (wird also kleiner bis zu einem bestimmten Winkel).
Eines der beiden Rechtecke ist immer gerade.(x-werte der linken/rechten punkte sind jeweils gleich)
Gegeben sind die Punkte der Ursprungsrechtecke (ungedreht,gedreht).
Das Zielrechteck liegt auch waagerecht im Koordinatensystem
Hat jemand schon mal so etwas gemacht?
Wie kann ich da rangehen?
Das kann man sicher irgendwie als Extremwertaufgabe lösen. Ist aber schon zu lange her, als das ich mich erinnern würde.
Ich suche einen Algorithmus zum berechnen eines Rechtecks, welches den maximalen Flächeninhalt zweier übereinanderliegenden Rechtecke hat.
Beispiel:
2 Rechtecke der selben Größe (ja, immer der selben Größe), liegen anfangs genau aufeinander. Wenn ich den Algorithmus nun anwende, sollte dieser mir ein Rechteck von der Größe der anderen beiden zurückgeben.
Jetzt drehe ich eines der beiden Rechtecke um X Grad um den Mittelpunkt von sich selbst.
Nun soll der Algorithmus mir die Koordinaten eines Rechtecks zurückgeben. Dieses Rechteck darf nur aus einer Fläche bestehen, welche das gedrehte Ursprungsrechteck vollständig enthält (wird also kleiner bis zu einem bestimmten Winkel).
Eines der beiden Rechtecke ist immer gerade.(x-werte der linken/rechten punkte sind jeweils gleich)
Gegeben sind die Punkte der Ursprungsrechtecke (ungedreht,gedreht).
Das Zielrechteck liegt auch waagerecht im Koordinatensystem
Hat jemand schon mal so etwas gemacht?
Wie kann ich da rangehen?
Das kann man sicher irgendwie als Extremwertaufgabe lösen. Ist aber schon zu lange her, als das ich mich erinnern würde.
Zuletzt bearbeitet: