Hallo.
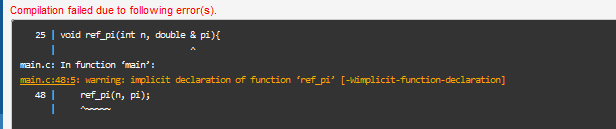
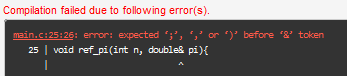
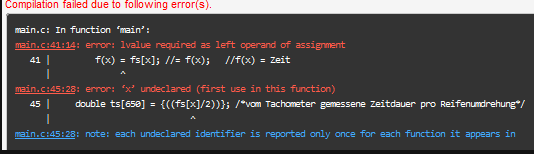
Ich habe hier die Leibnitz-Reihe und muss noch dazu eine Funktion Schreiben wo der Näherungswert der Leibnitz-Reihe als Referenzparameter in die main übergeben wird. Und die Funktion darf keinen Rückgabewert haben.
Leider denke ich immer in zu komplizierten Schritten und habe jetzt ein Blackout.
Kann mir einer Helfe.
Ich habe hier die Leibnitz-Reihe und muss noch dazu eine Funktion Schreiben wo der Näherungswert der Leibnitz-Reihe als Referenzparameter in die main übergeben wird. Und die Funktion darf keinen Rückgabewert haben.
Leider denke ich immer in zu komplizierten Schritten und habe jetzt ein Blackout.
Kann mir einer Helfe.
C:
#include<stdio.h>
#include<math.h>
double gesucht (int n)
{
long int i;
double sum=0.0, term, pi;
for(i=0;i< n;i++)
{
term = pow(-1, i) / (2*i+1);
sum += term;
}
pi = 4 * sum;
return pi;
}
int main()
{
long int n;
double pi;
printf("Wie viele Durchläufe soll es werden? Bitte eingeben:");
scanf("%ld", &n);
pi = gesucht (n);
printf("\nPI = %.6lf", pi);
return 0;
}
Zuletzt bearbeitet: